- 11.06.2015
- 685
- 0
Рабочие листы
к вашим урокам
Скачать
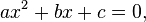
где 
— свободная переменная, 
, 
, 
— коэффициенты, причём 
Выражение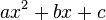 
называют квадратным трёхчленом.
Корень — это значение переменной , обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Элементы квадратного уравнения имеют собственные названия:
называют первым или старшим коэффициентом, называют вторым или коэффициентом при , называют свободным членом.Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент :
6 663 247 материалов в базе
Настоящий материал опубликован пользователем Красноперова Ирина Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Удалить материал
Ваша скидка на курсы
40%
Курс профессиональной переподготовки
500/1000 ч.
Курс повышения квалификации
72 ч. — 180 ч.
Курс повышения квалификации
72 ч. — 180 ч.
Курс повышения квалификации
36 ч. — 180 ч.
Мини-курс
4 ч.
Мини-курс
4 ч.
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.