
Рабочие листы
к вашим урокам
Скачать

1 слайд
Решение задач
на готовых чертежах.
Теорема Пифагора.
Геометрия.
8 класс.
Каратанова Марина Николаевна
МОУ СОШ №256 г.Фокино

2 слайд
8
9
10
11
12
14
15
16
17
18
20
21
22
23
24
30
29
28
27
26
1
2
3
4
5
6
13
19
25
7

3 слайд
1.
Найти:
С
В
А
Дано:
8 см
6 см
?

4 слайд
2.
Дано:
С
В
Найти:
А
5 см
7 см
?

5 слайд
3.
Дано:
Найти:
А
B
C
D
?
12 см
13 см

6 слайд
4.
Дано:
Найти:
В
А
С
О
D
2
?

7 слайд
5.
Дано:
А
B
C
D
Найти:
5 см
?

8 слайд
6.
Дано:
Найти:
А
B
C
1350
1350
6 см
?

9 слайд
7.
Найти:
Дано:
А
B
C
D
Е
450
6
?

10 слайд
8.
Найти:
Дано:
А
B
C
D
10
6
Е
?

11 слайд
9.
Дано:
Найти:
А
B
C
D
E
F
300
4

12 слайд
10.
Дано:
Найти:
А
B
C
D
6
8

13 слайд
11.
Найти:
Дано:
А
B
C
D
a
O
?

14 слайд
12.
Найти:
Дано:
А
B
C
D
4
300

15 слайд
13.
Найти:
Дано:
А
B
C
8
D
6

16 слайд
14.
Дано:
А
B
C
D
E
8
450
Найти:
300

17 слайд
15.
Дано:
Найти:
А
C
B
D
O
E
4

18 слайд
16.
Дано:
А
B
C
20
Найти:
450
450

19 слайд
17.
А
B
C
D
Дано:
Найти:
О
?

20 слайд
18.
Дано:
Найти:
B
C
6
300
А

21 слайд
19.
Найти:
Дано:
B
C
D
13
5
17
А
Доп.
Е

22 слайд
20.
Найти:
Дано:
B
C
D
15
9
20
А
К
Доп.

23 слайд
21.
Найти:
Дано:
А
B
C
D
450
Доп.
12
10

24 слайд
22.
Найти:
Дано:
А
B
C
Н
600
8
12
Доп.

25 слайд
23.
Найти:
Дано:
А
C
В
D
24
1

26 слайд
24.
Найти:
Дано:
А
C
В
М
12
9

27 слайд
25.
Найти:
Дано:
А
B
C
D
О
К

28 слайд
26.
Найти:
Дано:
А
B
C
М
K
17
N
Доп.
17

29 слайд
27.
Найти:
Дано:
А
B
C
D
H
27
13
10
300
Доп.

30 слайд
28.
Найти:
А
B
C
14
Дано:
13
15

31 слайд
29.
Найти:
Дано:
А
B
C
D
9
12
15

32 слайд
30.
Найти:
Дано:
А
B
C
D
H
11
7
9
12
Доп.

Рабочие листы
к вашим урокам
Скачать
Геометрическая формулировка.
Изначально теорема была сформулирована следующим образом:
|
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. |
Алгебраическая формулировка.
|
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. |
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора.
Для всякой тройки положительных чисел a, b и c, такой, что a2+b2=c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы [1]. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).
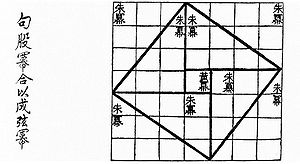
Традиционно авторство теоремы приписывают греческому философу и математику Пифагору, хотя есть свидетельства того, что теорема была известна задолго до него в Вавилоне и Древнем Китае. Возможно, Пифагор и узнал эту теорему во время своего путешествия по Египту и Вавилону, а может быть, и в Милетской школе. Однако есть свидетельства, что доказательство теоремы впервые было приведено именно им, или , по крайней мере, в его школе. Существует исторический анекдот и легенда, что когда Пифагор окрыл свою теорему, он в благодарность богам принёс в жертву 100 быков, и с тех пор все скоты ненавидят математику. Открытие и понимание теоремы протекало в несколько этапов:
Согласно комментариям Прокла к трудам Евклида, Пифагор (569—475 гг. до н. э.), использовал алгебраические методы для конструкции Пифагоровых троек. Комментарии Прокла датируются 410 и 485 годами до н. э. соответственно. Примечательно, что известный английский историк математики Хиф (Heath), полагает, что не существует убедительных доказательств в пользу Пифагора на протяжении 5 столетий после его жизни на предмет авторства теоремы. В то же время, такие известные авторы, как Плутарх и Цицерон, приписывают авторство теоремы именно Пифагору, в соответствии с этими источниками можно сделать вывод о том, что авторство Пифагора было широко известно и не подвергалось сомнению.
6 663 054 материала в базе

Настоящий материал опубликован пользователем Григорьева Галина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Удалить материалВаша скидка на курсы
40%Курс повышения квалификации
36 ч. — 144 ч.
Курс профессиональной переподготовки
300/600 ч.
Курс повышения квалификации
36 ч. — 180 ч.
Мини-курс
10 ч.
Мини-курс
6 ч.
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.