Справочник по теме "Производная и графики в заданиях профильного ЕГЭ"

Справочник

Задание №7 профильная математика

Производной функции y=f(x)в точке x₀ называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю. То есть,

  

Геометрический смысл производной	Физический смысл производной
Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке (тангенсу угла между касательной и осью Ох) f’(хo) = k = tg α	Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки: V(t)=x’(t)
•      Если f’(x) > 0 на промежутке, то функция f(x)  возрастает на этом  промежутке. Если f’(x) < 0 на промежутке, то функция f(x) убывает на этом промежутке	•      Если функция f(x)  возрастает на промежутке, то  f’(x) > 0 на этом  промежутке. Если функция f(x) убывает на промежутке, то f’(x) < 0 на этом промежутке
Если прямые параллельны, то их угловые коэффициенты равны
•      Точка хo называется точкой максимума функции f(х), если  существует такая окрестность точки хo, что для всех х≠ хo из этой окрестности выполняется неравенство f(х) < f(хo). •      Точка хo называется точкой минимума функции f(х), если существует такая окрестность точки хo, что для всех х≠ хo из этой  окрестности выполняется неравенство f(х) > f(хo) = 0. •      Если хo – точка экстремума функции f(х), то f’(хo) = 0.	Пусть функция f(х) дифференцируема на интервале (a;b), хo Є (a; b)   и  f’(хo) = 0, то: •  при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «плюса» на «минус», то хo – точка максимума функции f(х); •  при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «минуса» на «плюс», то хo – точка минимума функции f(х).

Примеры заданий

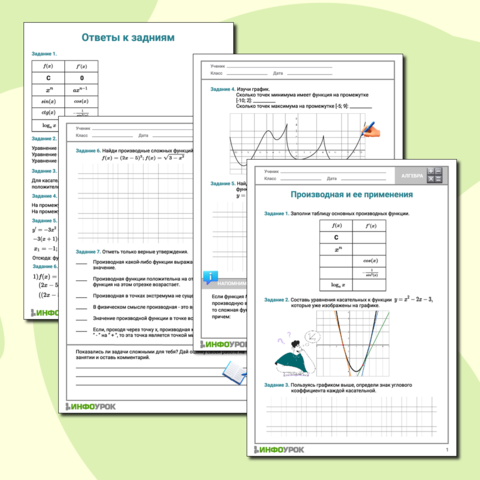
№	Задание	Что делать?
1.	На рисунке изображен график функции y=f(x) и касательная к нему в точке х0. Найдите значение производной функции f(x) в точке x0.	Найти тангенс угла наклона касательной к оси абсцисс (отношение противолежащего катета к прилежащему катету). На рисунке выделены точки на касательной, на которых как на гипотенузе надо достроить прямоугольный треугольник. Если α <900, то tg α >0, если α >900, то tg α <0.
2.	На рисунке изображен график функции y=f(x), определённый на интервале (-10;2). Найдите количество точек, в которых производная функции f(x) равна 0.	Подсчитать количество точек экстремума(минимумы и максимумы)
3.	На рисунке изображен график функции y=f(x), определённый на интервале (-1;12). Найдите количество целых точек, в которых производная функции отрицательна.	Подсчитать целые точки на промежутках убывания функции
4.	На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.	x=-2, то f ↓ => f’ <0 x=-1, то f имеет экстремум =>f’=0 x=2, то f ↑ => f’ >0 x=3, то f ↓ => f’ <0
5.	На рисунке изображён график дифференцируемой функции y=f(x), и отмечены семь точек на оси абсцисс: х1, х2, х3, х4, х5, х6, х7, х8,х9 . В скольких из этих точек производная функции  f(x) отрицательна?	В скольких точках функция убывает
6.	На рисунке изображен график функции y=f’(x ) – производной функции f(x), определённой на интервале (-6;5). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.	Промежутки убывания функции =производная на данном графике отрицательна, т.е.расположена ниже оси Ох. Найти сумму целых точек.
7.	На рисунке изображен график функции y=f’(x ) – производной функции f(x), определённой на интервале (-8;6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.	Промежутки возрастания функции =производная на данном графике положительна, т.е.расположена выше оси Ох. Записать длину большего промежутка
8.	На рисунке изображены график функции y=f’(x ) – производной функции f(x) и семь точек на оси абсцисс: х1, х2, х3, х4, х5, х6, х7. В скольких из этих точек функция  f(x) возрастает?	Сосчитать количество точек, в которых производная на данном графике положительна
9.	Прямая y=6x+9 параллельна касательной к графику функции y=x2+7х-6. Найдите абсциссу точки касания.	Если прямые параллельны, то их угловые коэффициенты равны. Найти производную функции (x2+7х-6)’=2x+7=kкас=6 =>  x=-0,5
10.	Прямая y=-9x+5 параллельна касательной к графику функции y=аx2+15х+11. Найдите a.	Найти производную функции (аx2+15х+11)’=2a+15= -9 => a= -12
11.	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-9;3). Найдите количество точек, в которых касательная к графику f(x) параллельна прямой y=2x-19 или совпадает с ней.	Провести горизонтальную прямую y=2 и сосчитать количество точек пересечения с графиком.
12.	На рисунке изображён график функции y=f(x), определённой на интервале (-3;9). Найдите количество точек, в которых касательная к графику f(x) параллельна прямой y=12.	Т.к. угловой коэффициент прямой y=12 равен 0, то считаем количество точек пересечения с осью Ох.
13.	На рисунке изображен график производной функции y=f’(x). Найдите абсциссу точки, в которых касательная к графику функции y=f(x) параллельна оси абсцисс или  совпадает ней.	Находим точку на графике y=f’(x), в которой у=0, т.е.точку пересечения данного графика с осью Ох => -3
14.	На рисунке изображен график производной функции y=f’(x), определенной на интервале (-7;4). В какой точке отрезка [-6;-1] функция f(x) принимает наибольшее значение?	На отрезке [-6;-1] производная положительна (лежит выше Ох) => функция возрастает, т.е. достигает наибольшего значения при наибольшем значении аргумента => -1 Значит в х=-6 достигает наименьшего значения.
15.	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-7;4). Найдите точку максимума функции f(x).	Находим точку на оси Ох, в которой производная меняет свой знак с «+» на «-» => -1
16.	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-6;5). Найдите точку экстремума функции f(x), принадлежащую отрезку [-5;4].	Находим точку на оси Ох, в которой производная меняет свой знак =>  -2
17.	На рисунке изображён график функции y=f(x), определённой на интервале (-5;7). Найдите сумму точек экстремума функции f(x).	Считаем сумму «горбов и впадин» по оси Ох: -3 + (-1) +0+2+3+5+6=12
18.	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-10;8). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-9;6].	Находим точки на оси Ох, в которой производная меняет свой знак  с  «+» на «-» =>  х= -4 и х=4 => 2
19.	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-16;4). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-14;2].	Считаем количество точек пересечения графика производной на рисунке с осью Ох => 5
20.	Материальная точка движется прямолинейно по закону x(t)=t2-3t-29, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=3с.	V(t=3)=x’(t)=( t2-3t-29)’= =2t-3=2*3-3=3
21.	Материальная точка движется прямолинейно по закону x(t)=1/6t3-2t2-4t+39, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равной 38м/с.	V(t)=x’(t)=( 1/6t3-2t2-4t+39)’= =1/6 *3t2-2*2t-4=0.5t-4t-4 Если V=38, то 0.5t2-4t-4=38                         0.5t2-4t-4-38=0                        t2-8t-84=0 Решая уравнение через D, находим t=14

Краткое описание документа:

Часто учащиеся путаются при выполнении задания №7 Профильной математики ЕГЭ. Я постаралась собрать прототипы заданий и мои рекомендации к ним "на языке учеников". Материал содержит краткую теорию по разделу "Применение производной к исследованию графиков". Учебник содержит недостаточно заданий типа №7 Профильного ЕГЭ.