Тема урока "Понятие многогранника."

Тема: Понятие многогранника.

Цель урока: ознакомить учащихся с понятием многогранника, элементами многогранника, рассмотреть теорему Эйлера.

Задачи:

- обучающие: ввести понятие многогранника и его элементов

-развивающие: развитие логического мышления, внимания, памяти, кругозора;

-воспитательные: формирование навыков самоконтроля и взаимоконтроля.

Ход урока:

I этап: Организационный момент, приветствие

II этап: Новая тема:

Начнем с определения многогранника:

Многогранник — это такое тело, поверхность которого составлена из многоугольников. Эти многоугольники называются гранями многогранника, их стороны — ребрами, а вершины — вершинами многогранника.

Возьмем в пространстве фигуру, например куб (рис 1) Куб состоит из точек. Его точка А расположенная внутри куба, она окружена только точками, принадлежащими кубу (изобразим это окружение маленькой сферой). Такие точки назовем внутренними. Точка С расположенная вне куба, окружена точками не принадлежащими кубу. Такие точки назовем внешними. Точка В принадлежит ребру куба, окружена сферой, которая содержит и внутренние точки куба, и внешние его точки. Такие точки называются граничными, а множество всех граничных точек образуют границу куба.

Например: поверхность куба — его граница, сфера — граница шара.

Если любые две внутренние точки фигуры можно соединить ломанной, соединяющей только внутренние точки фигуры, то множество всех внутренних точек фигуры называется ее внутренней областью.

Объединение границы и внутренней области называется замкнутой областью.

Телом называется пространственная замкнутая область, если она ограничена, поверхность тела — его граница.

Опираясь на понятие тела, можно определить понятие многогранника.

Определение: Многогранником называется тело, поверхностью которого является объединение конечного числа многоугольников.

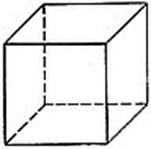Рисунок 1

Многогранник обозначают буквами, которые поставлены у всех его вершин.

По числу граней различают четырехгранник (треугольная пирамида) (рис 2), пятигранник (рис 3), восьмигранник (октаэдр) (рис 4)

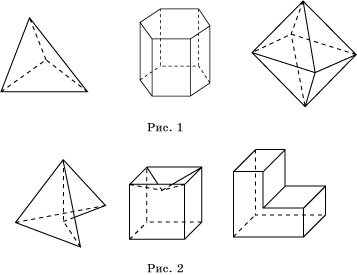
Многогранники также бывают выпуклыми и невыпуклыми.

Определение: Многогранник называется выпуклым, если он расположен целиком по одну сторону от любой из плоскостей , содержащих его границ.

Куб и прямоугольный параллелепипед — примеры выпуклых многогранников. (Рис 1)

(рис 2) примеры невыпуклого многогранника

III этап: подведение итогов

IV этап: домашнее задание параграф 1.3 стр 7